109. Convert Sorted List to Binary Search Tree
1. Description
Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
2. Example
Example 1:
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.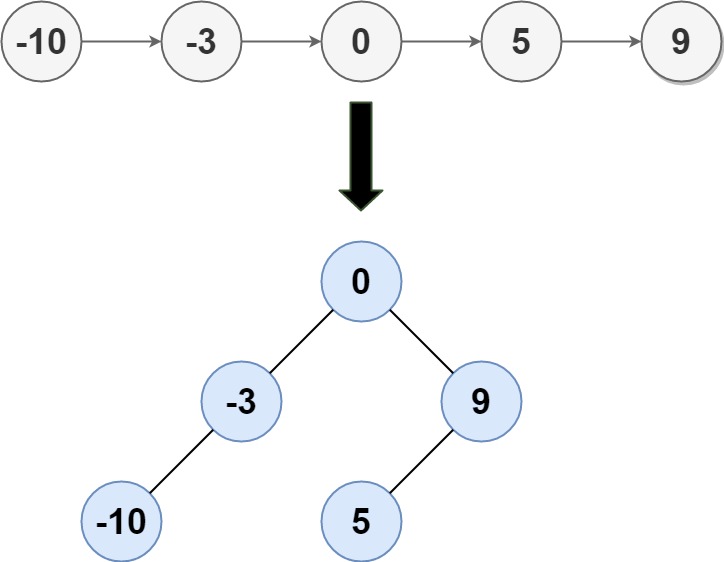
Example 2:
Input: head = []
Output: []
Example 3:
Input: head = [0]
Output: [0]
Example 4:
Input: head = [1,3]
Output: [3,1]
3. Constraints
- The number of nodes in head is in the range [0, $2 * 10^4$].
- $-10^5$ <= Node.val <= $10^5$
4. Solutions
My Accepted Solution
n is the number of nodes in i_head
Time complexity: O(n)
Space complexity: O($log_2n$) or O(n) with the result’s space
// Divide and Conquer && Recursion $$ In-order Iteration
class Solution {
public:
// TreeNode *sortedListToBST(ListNode *head)
TreeNode *sortedListToBST(ListNode *i_head) {
ListNode *iter = i_head;
int listLength = getListLength(i_head);
return sortedListToBST(iter, 0, listLength - 1);
}
private:
int getListLength(const ListNode *i_head) {
int length = 0;
for (auto iter = i_head; iter; iter = iter->next) {
++length;
}
return length;
}
TreeNode *sortedListToBST(ListNode *&m_head, int left, int right) {
if (left > right) {
return nullptr;
}
int middle = (left + right + 1) / 2;
TreeNode *root = new TreeNode();
root->left = sortedListToBST(m_head, left, middle - 1);
root->val = m_head->val;
m_head = m_head->next;
root->right = sortedListToBST(m_head, middle + 1, right);
return root;
}
};