124. Binary Tree Maximum Path Sum

1. Description

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node’s values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.

2. Example

Example 1: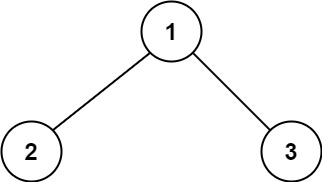

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2: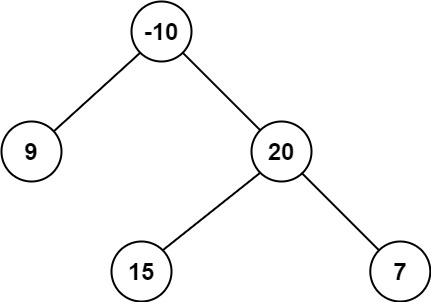

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

3. Constraints

• The number of nodes in the tree is in the range [1, $3 * 10^4$].
• -1000 <= Node.val <= 1000

4. Solutions

Depth-First Search

n is the number of nodes in root
Time complexity: O(n)
Space complexity: O(n)

class Solution {
public:
    int maxPathSum(TreeNode *root) {
        traverse_(root);

        return max_sum_;
    }

private:
    int max_sum_ = INT_MIN;

    int traverse_(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        int left_child_sum = traverse_(root->left);
        int right_child_sum = traverse_(root->right);

        max_sum_ = max(max_sum_, max(left_child_sum, 0) + max(right_child_sum, 0) + root->val);

        return max(0, max({0, left_child_sum, right_child_sum}) + root->val);
    }
};