1372. Longest ZigZag Path in a Binary Tree

1. Description

You are given the root of a binary tree.
A ZigZag path for a binary tree is defined as follow:

• Choose any node in the binary tree and a direction (right or left).
• If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
• Change the direction from right to left or from left to right.
• Repeat the second and third steps until you can’t move in the tree.

Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return the longest ZigZag path contained in that tree.

2. Example

Example 1

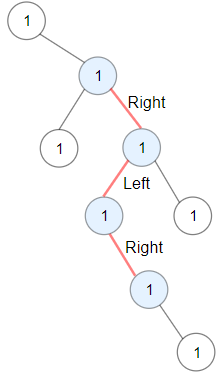
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2

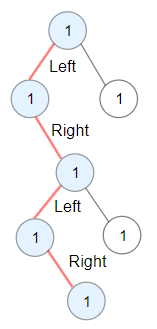
Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3

Input: root = [1]
Output: 0

3. Constraints

• The number of nodes in the tree is in the range [1, 5 * $10^4$].
• 1 <= Node.val <= 100

4. Solutions

Depth-First Search

n is the number of nodes in root
Time complexity: O(n)
Space complexity: O(n)

class Solution {
public:
    int longestZigZag(TreeNode *root) {
        int longest_path = 0;
        search_longest_zigzag(root->left, 0, 1, longest_path);
        search_longest_zigzag(root->right, 0, 1, longest_path);

        return longest_path;
    }

private:
    void search_longest_zigzag(TreeNode *root, int direction, int length, int &longest_path) {
        if (root != nullptr) {
            longest_path = max(length, longest_path);

            search_longest_zigzag(root->left, 0, direction == 1 ? length + 1 : 1, longest_path);
            search_longest_zigzag(root->right, 1, direction == 0 ? length + 1 : 1, longest_path);
        }
    }
};