1466. Reorder Routes to Make All Paths Lead to the City Zero

1. Description

There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by connections where connections[i] = [$a_i$, $b_i$] represents a road from city $a_i$ to city $b_i$.
This year, there will be a big event in the capital (city 0), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.
It’s guaranteed that each city can reach city 0 after reorder.

2. Example

Example 1

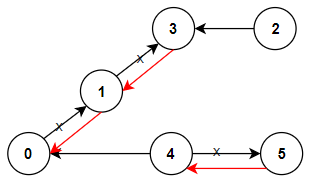
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 2

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 3

Input: n = 3, connections = [[1,0],[2,0]]
Output: 0

3. Constraints

• 2 <= n <= 5 * $10^4$
• connections.length == n - 1
• connections[i].length == 2
• 0 <= $a_i$, $b_i$ <= n - 1
• $a_i$ != $b_i$

4. Solutions

Depth-First Search

Time complexity: O(n)
Space complexity: O(n)

class Solution {
public:
    int minReorder(int n, vector<vector<int>> &connections) {
        // pair<to, needs_reorder>: needs_reorder == 1 if original edge is current -> to
        vector<vector<pair<int, uint8_t>>> edges(n);
        for (const auto &conn : connections) {
            edges[conn[0]].push_back(make_pair(conn[1], 1));
            edges[conn[1]].push_back(make_pair(conn[0], 0));
        }

        return traverse(-1, 0, edges);
    }

private:
    int traverse(int parent, int current, vector<vector<pair<int, uint8_t>>> &edges) {
        int reorder_count = 0;
        for (auto &edge : edges[current]) {
            if (edge.first != parent) {
                reorder_count += edge.second + traverse(current, edge.first, edges);
            }
        }

        return reorder_count;
    }
};