160. Intersection of Two Linked Lists

1. Description

Write a program to find the node at which the intersection of two singly linked lists begins.
For example, the following two linked lists: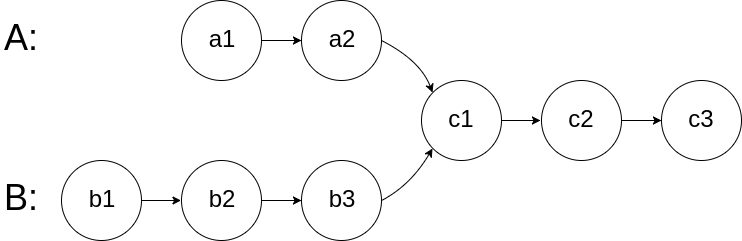

begin to intersect at node c1.

2. Example

Example 1:
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value = 8
Input Explanation: The intersected node’s value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.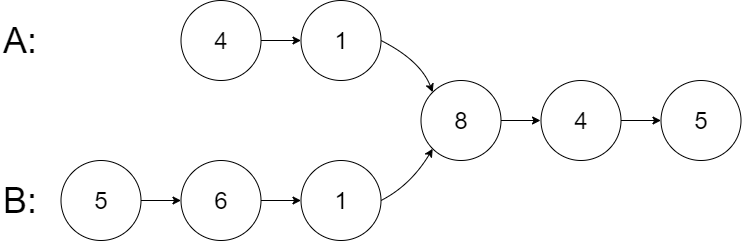

Example 2:
Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Reference of the node with value = 2
Input Explanation: The intersected node’s value is 2 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.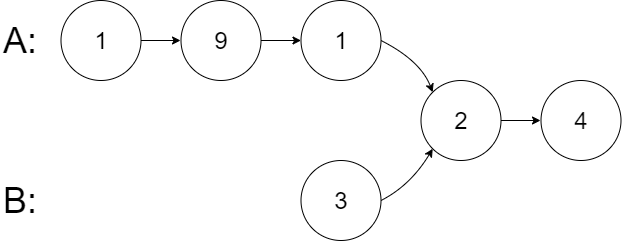

Example 3:
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null
Input Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.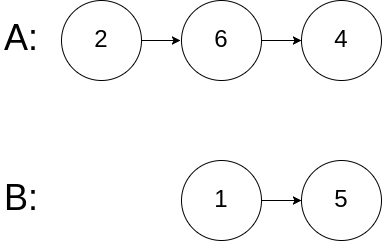

3. Notes

• If the two linked lists have no intersection at all, return null.
• The linked lists must retain their original structure after the function returns.
• You may assume there are no cycles anywhere in the entire linked structure.
• Each value on each linked list is in the range [1, $10^9$].
• Your code should preferably run in O(n) time and use only O(1) memory.

4. Solutions

My Accepted Solution

n is the max number of nodes in m_head1 and m_head2
Time complexity: O(n)
Space complexity: O(1)

// we get two lists' length, and let the longer one pass additional nodes, then, move together with the shorter one
// they will meet the common node

class Solution 
{
public:
    // ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
    ListNode *getIntersectionNode(ListNode *m_head1, ListNode *m_head2) 
    {
        int list1Length = 0;
        for(auto iter = m_head1; iter; iter = iter->next) list1Length++;
        int list2Length = 0;
        for(auto iter = m_head2; iter; iter = iter->next) list2Length++;

        if(list1Length < list2Length)
        {
            swap(m_head1, m_head2);
            swap(list1Length, list2Length);
        }
 
        for(auto iter1 = m_head1, iter2 = m_head2; iter1 && iter2; )
        {
            if(list1Length > list2Length)
            {
                list1Length--;
                iter1 = iter1->next;
            }
            else
            {
                if(iter1 == iter2) return iter1;
                
                iter1 = iter1->next;
                iter2 = iter2->next;
            }
        }

        return nullptr;
    }
};

4.1 Two Pointers

m is the number of nodes in m_head1, n is the number of nodes in m_head2
Time complexity: O(m + n)
Space complexity: O(1)

// length(A) + length(B) == length(B) + length(A)
// so we finish the iteration of one list, we continue to iterate the other one
// and we will find the common node

class Solution 
{
public:
    // ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
    ListNode *getIntersectionNode(ListNode *m_head1, ListNode *m_head2) 
    {
        if(!m_head1 || !m_head2) return nullptr;
        
        for(auto iter1 = m_head1, iter2 = m_head2; iter1 || iter2; iter1 = iter1->next, iter2 = iter2->next)
        {
            if(!iter1) iter1 = m_head2;
            if(!iter2) iter2 = m_head1;
            
            if(iter1 == iter2) return iter1;   
        }

        return nullptr;
    }
};