25. Reverse Nodes in k-Group
1. Description
Given a linked list, reverse the nodes of a linked list k at a time and return its modified list.
k is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of k then left-out nodes, in the end, should remain as it is.
2. Follow Up
- Could you solve the problem in O(1) extra memory space?
- You may not alter the values in the list’s nodes, only nodes itself may be changed.
3. Example
Example 1:
Input: head = [1,2,3,4,5], k = 2
Output: [2,1,4,3,5]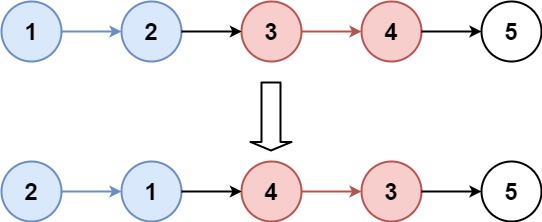
Example 2:
Input: head = [1,2,3,4,5], k = 3
Output: [3,2,1,4,5]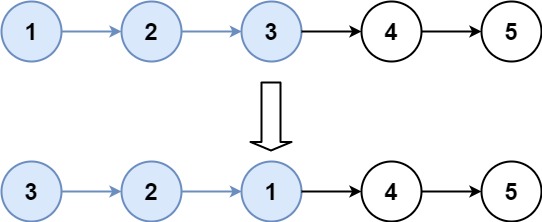
Example 3:
Input: head = [1,2,3,4,5], k = 1
Output: [1,2,3,4,5]
Example 4:
Input: head = [1], k = 1
Output: [1]
4. Constraints
- The number of nodes in the list is in the range sz.
- 1 <= sz <= 5000
- 0 <= Node.val <= 1000
- 1 <= k <= sz
5. Solutions
My Accepted Solution(Follow Up)
n is the number of nodes in m_head
Time complexity: O(n)
Space complexity: O(1)
Like 206. Reverse Linked List, we just need to reverse nodes every k nodes.
class Solution {
public:
// ListNode* reverseKGroup(ListNode* head, int k)
ListNode* reverseKGroup(ListNode *m_head, int k) {
auto guardHead = new ListNode();
auto left = m_head, right = m_head, head = guardHead, last = m_head;
while (m_head != nullptr) {
for (int i = 1; i < k && right != nullptr; i++) {
right = right->next;
}
if (right != nullptr) {
head->next = right;
head = left;
auto iter = left->next, prev = left, nextGroup = right->next;
for (int i = 1; i < k; i++) {
auto temp = iter->next;
iter->next = prev;
prev = iter;
iter = temp;
}
left->next = nullptr;
last = left = right = m_head = nextGroup;
} else {
head->next = left;
break;
}
}
return guardHead->next;
}
};
