501. Find Mode in Binary Search Tree
1. Description
Given the root of a binary search tree (BST) with duplicates, return all the mode(s) (i.e., the most frequently occurred element) in it.
If the tree has more than one mode, return them in any order.
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than or equal to the node’s key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
- Both the left and right subtrees must also be binary search trees.
2. Example
Example 1: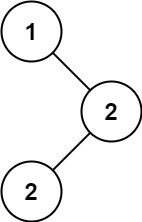
Input: root = [1,null,2,2]
Output: [2]
Example 2:
Input: root = [0]
Output: [0]
3. Constraints
- The number of nodes in the tree is in the range [1, ].
- <= Node.val <=
4. Follow Up
Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
5. Solutions
Binary Search Tree(Follow Up)
n is the number of nodes in root
Time complexity: O(n)
Space complexity: O(1)
// the follow up may ask us to use Morris iteration, which will change the input data
// so I don't like it
class Solution {
public:
vector<int> findMode(const TreeNode *root) {
vector<int> result;
pre_order_iter_(root, result);
return result;
}
private:
int current_number_ = INT_MAX;
int occur_count_ = INT_MIN;
int max_occur_count_ = INT_MIN;
void check_number_(int number, vector<int> &result) {
if (number == current_number_) {
++occur_count_;
} else {
occur_count_ = 1;
current_number_ = number;
}
if (occur_count_ == max_occur_count_) {
result.push_back(number);
} else if (occur_count_ > max_occur_count_) {
max_occur_count_ = occur_count_;
result = {number};
}
}
void pre_order_iter_(const TreeNode *root, vector<int> &result) {
if (root != nullptr) {
pre_order_iter_(root->left, result);
check_number_(root->val, result);
pre_order_iter_(root->right, result);
}
}
};
