563. Binary Tree Tilt

1. Description

Given the root of a binary tree, return the sum of every tree node’s tilt.
The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.

2. Example

Example 1: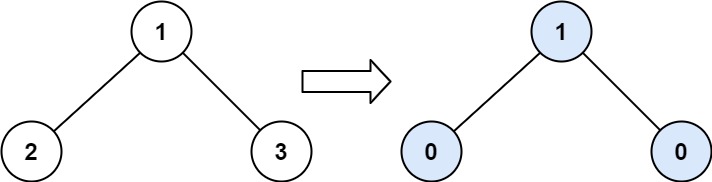

Input: root = [1,2,3]
Output: 1
Explanation:
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

Example 2: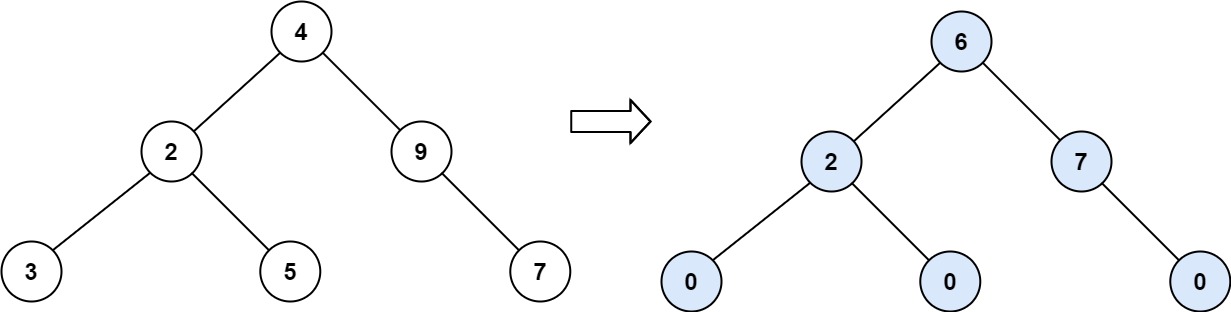

Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation:
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

Example 3: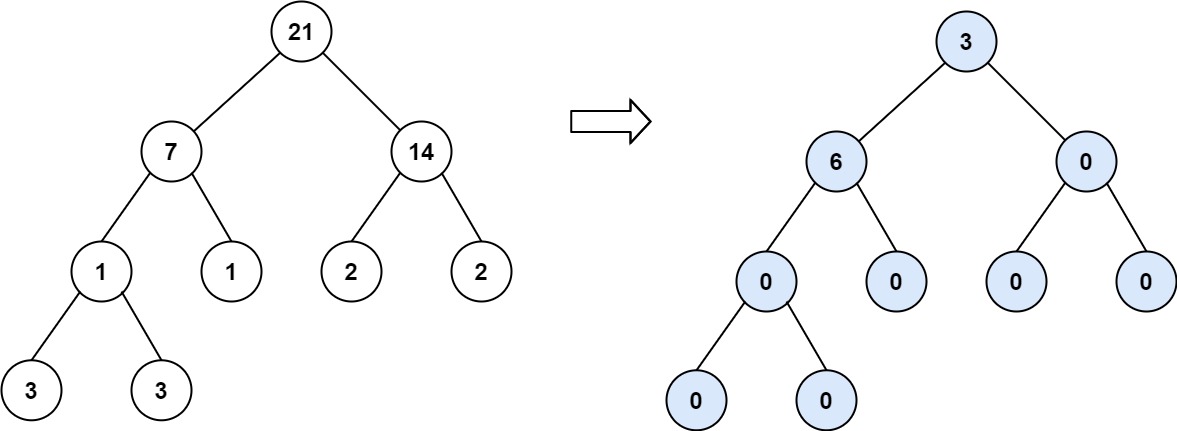

Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

3. Constraints

• The number of nodes in the tree is in the range [0, $10^4$].
• -1000 <= Node.val <= 1000

4. Solutions

Depth-First Search

n is the number of nodes in root
Time complexity: O(n)
Space complexity: O(n)

class Solution {
public:
    int findTilt(TreeNode *root) {
        traverse_(root);

        return sum_;
    }

private:
    int sum_ = 0;
    int traverse_(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        int left_sum = traverse_(root->left);
        int right_sum = traverse_(root->right);
        int sum = root->val + left_sum + right_sum;

        root->val = abs(left_sum - right_sum);
        sum_ += root->val;

        return sum;
    }
};