598. Range Addition II

1. Description

You are given an m x n matrix M initialized with all 0’s and an array of operations ops, where ops[i] = [ai, bi] means M[x][y] should be incremented by one for all 0 <= x < ai and 0 <= y < bi.
Count and return the number of maximum integers in the matrix after performing all the operations.

2. Example

Example 1:
Input: m = 3, n = 3, ops = [[2,2],[3,3]]
Output: 4
Explanation: The maximum integer in M is 2, and there are four of it in M. So return 4.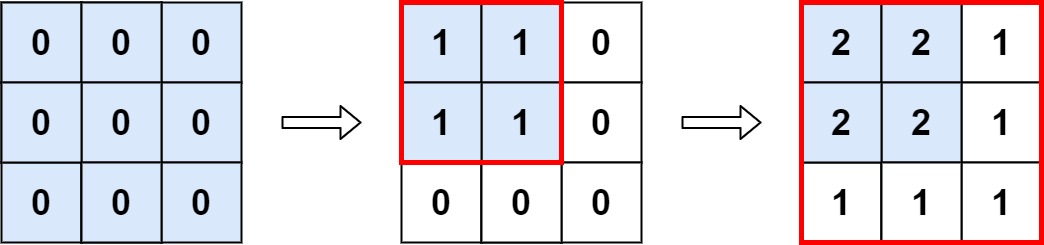

Example 2:
Input: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
Output: 4

Example 3:
Input: m = 3, n = 3, ops = []
Output: 9

3. Constraints

• 1 <= m, n <= $4 * 10^4$
• 1 <= ops.length <= $10^4$
• ops[i].length == 2
• 1 <= ai <= m
• 1 <= bi <= n

4. Solutions

My Accepted Solution

n = i_operations.size()
Time complexity: O(n)
Space complexity: O(1)

// every operation will give a matrix, and numbers with the max value must run all operations
// so, numbers with the max value are the duplicate area of all operations
// so, we just need to record a row and colum, which is used to record min area of all operations' coverage

class Solution 
{
public:
    // int maxCount(int m, int n, vector<vector<int>>& ops)
    int maxCount(int row, int colum, vector<vector<int>> &i_operations) 
    {
        for(int i = 0; i < i_operations.size(); i++)
        {
            row = min(row, i_operations[i].front());
            colum = min(colum, i_operations[i].back());
        }
        
        return row * colum;
    }
};