655. Print Binary Tree

1. Description

Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:

• The height of the tree is height and the number of rows m should be equal to height + 1.
• The number of columns n should be equal to 2height+1 - 1.
• Place the root node in the middle of the top row (more formally, at location res[0][(n-1)/2]).
• For each node that has been placed in the matrix at position res[r][c], place its left child at res[r+1][c-2height-r-1] and its right child at res[r+1][c+2height-r-1].
• Continue this process until all the nodes in the tree have been placed.
• Any empty cells should contain the empty string “”.

Return the constructed matrix res.

2. Example

Example 1: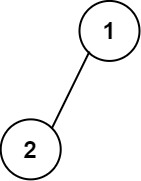

Input: root = [1,2]
Output:
[["",“1”,""],
[“2”,"",""]]

Example 2: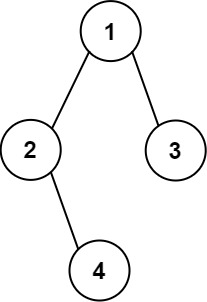

Input: root = [1,2,3,null,4]
Output:
[["","","",“1”,"","",""],
["",“2”,"","","",“3”,""],
["","",“4”,"","","",""]]

3. Constraints

• The number of nodes in the tree is in the range [1, $2^{10}$].
• -99 <= Node.val <= 99
• The depth of the tree will be in the range [1, 10].

4. Solutions

Depth-First Search

n is the height root
Time complexity: O($n2^n$)
Space complexity: O(n)

class Solution {
public:
    vector<vector<string>> printTree(TreeNode *root) {
        int height = get_height_(root);
        int n = (1 << height) - 1;
        vector<vector<string>> result(height, vector<string>(n));
        traverse_(root, height, result, 0, (n - 1) >> 1);

        return result;
    }

private:
    int get_height_(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        return 1 + max(get_height_(root->left), get_height_(root->right));
    }

    void traverse_(TreeNode *root, const int height, vector<vector<string>> &result, int i, int j) {
        if (root != nullptr) {
            result[i][j] = to_string(root->val);

            if (i + 1 < height) {
                traverse_(root->left, height, result, i + 1, j - (1 << (height - i - 1 - 1)));
                traverse_(root->right, height, result, i + 1, j + (1 << (height - i - 1 - 1)));
            }
        }
    }
};