766. Toeplitz Matrix

2020, Dec 05 3 mins read

1. Description

Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false.
A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.

2. Example

Example 1:
Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
Output: true
Explanation:
In the above grid, the diagonals are:
“[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”.
In each diagonal all elements are the same, so the answer is True.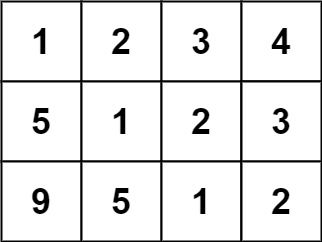

Example 2:
Input: matrix = [[1,2],[2,2]]
Output: false
Explanation:
The diagonal “[1, 2]” has different elements.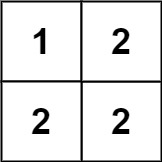

3. Constraints

m == matrix.length
n == matrix[i].length
1 <= m, n <= 20
0 <= matrix[i][j] <= 99

4. Follow Up

What if the matrix is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
What if the matrix is so large that you can only load up a partial row into the memory at once?

5. Solutions

My Accepted Solution

n is the number of elements in i_matrix
Time complexity: O(n)
Space complexity: O(1)

class Solution 
{
public:
    // bool isToeplitzMatrix(vector<vector<int>>& matrix)
    bool isToeplitzMatrix(vector<vector<int>> &i_matrix) 
    {
        for(int i = 1; i < i_matrix.size(); i++)
        {
            for(int j = 1; j < i_matrix.front().size(); j++)
            {
                if(i_matrix[i][j] != i_matrix[i - 1][j - 1])
                    return false;
            }
        }
        
        return true;
    }
};

5.1 XOR(Follow Up)

（异或）每次只加载一行，即不同时使用第i行和第i-1行的元素进行比较

n is the number of elements in i_matrix
Time complexity: O(n)
Space complexity: O(1)

// if the matrix only has one colum, it is valid
// if the matrix has two colums, we need to check whether it is equal to its left-up element
// if the matrix has more colums, such as 5 colums like [1, 2, 3, 4, 5]
// the last element, 5, is useless, it will not be any element's left-up element
// to save memory, we use xor to store the last row element, it is 12 ^ 23 ^ 34
// in this way, we could store every element's value and their orders in the same time
// so, in the next row, we just use the same methord to get a result and compare them

class Solution 
{
public:
    // bool isToeplitzMatrix(vector<vector<int>>& matrix)
    bool isToeplitzMatrix(vector<vector<int>> &i_matrix) 
    {
        if(i_matrix.front().size() == 1)
        {
            return true;
        }
        else if(i_matrix.front().size() == 2)
        {
            for(int i = 1; i < i_matrix.size(); i++)
            {
                if(i_matrix[i][1] != i_matrix[i - 1][0])
                    return false;
            }
            
            return true;
        }
        else
        {
            int xorSum = 0;
            for(int i = 1; i < i_matrix.front().size() - 1; i++)
                xorSum ^= (i_matrix[0][i - 1] * 10 + i_matrix[0][i]);
            
            for(int i = 1; i < i_matrix.size(); i++)
            {
                int currentRowXorSum = 0;
                for(int j = 2; j < i_matrix.front().size(); j++)
                    currentRowXorSum ^= (i_matrix[i][j - 1] * 10 + i_matrix[i][j]);
                
                if(xorSum != currentRowXorSum) return false;
                
                xorSum ^= (i_matrix[i][0] * 10 + i_matrix[i][1]) ^ (i_matrix[i][i_matrix.front().size() - 2] * 10 + i_matrix[i][i_matrix.front().size() - 1]);
            }
            
            return true;
        }
    }
};

comments powered by Disqus