787. Cheapest Flights Within K Stops • Algorithm Solutions

1. Description

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [$from_i$, $to_i$, $price_i$] indicates that there is a flight from city $from_i$ to city $to_i$ with cost $price_i$.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

2. Example

Example 1: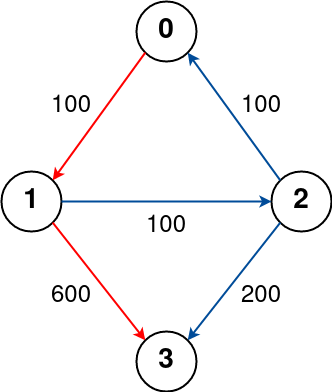
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

Example 2: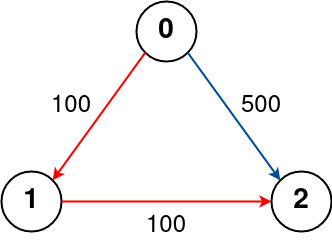
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

Example 3: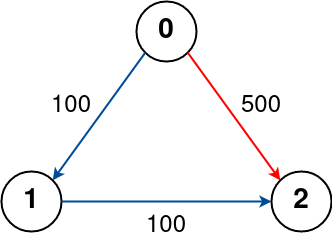
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

3. Constraints

1 <= n <= 100
0 <= flights.length <= (n * (n - 1) / 2)
flights[i].length == 3
0 <= $from_i$, $to_i$ < n
$from_i$ != $to_i$
1 <= $price_i$ <= $10^4$
There will not be any multiple flights between two cities.
0 <= src, dst, k < n
src != dst

4. Solutions

Breadth-First Search

m = flights.size(), n
Time complexity: I don’t know
Space complexity:

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>> &flights, int src, int dst, int k) {
        map<int, vector<pair<int, int>>> fly_dst_price;
        for (auto flight : flights) {
            fly_dst_price[flight[0]].emplace_back(flight[1], flight[2]);
        }

        queue<pair<int, int>> srcs{{{src, 0}}};
        vector<int> cheapest_from(n, INT_MAX);

        int cheapest_price = INT_MAX;
        for (int i = 0; i <= k; ++i) {
            int count = srcs.size();
            for (int j = 0; j < count; ++j) {
                auto node = srcs.front();
                srcs.pop();

                if (node.second < cheapest_from[node.first]) {
                    cheapest_from[node.first] = node.second;

                    for (auto dst_price : fly_dst_price[node.first]) {
                        srcs.push({dst_price.first, node.second + dst_price.second});

                        if (dst_price.first == dst) {
                            cheapest_price = min(cheapest_price, node.second + dst_price.second);
                        }
                    }
                }
            }
        }

        return cheapest_price == INT_MAX ? -1 : cheapest_price;
    }
};

Dynamic Programming

m = flights.size(), n
Time complexity: O((m+n)k)
Space complexity: O(n)

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>> &flights, int src, int dst, int k) {
        // dst_price[i] means from src to point i's price at the kth stop
        vector<int> dst_price(n, upper_bound_price_);
        dst_price[src] = 0;
        int cheapest_price = upper_bound_price_;
        for (int i = 0; i <= k; ++i) {
            vector<int> current_dst_price(n, upper_bound_price_);
            for (auto flight : flights) {
                int from = flight[0];
                int to = flight[1];
                int cost = flight[2];

                current_dst_price[to] = min(current_dst_price[to], dst_price[from] + cost);
            }
            dst_price = move(current_dst_price);
            cheapest_price = min(cheapest_price, dst_price[dst]);
        }

        return cheapest_price == upper_bound_price_ ? -1 : cheapest_price;
    }

private:
    // don't use INT_MAX, we need to add something to it
    const int upper_bound_price_ = 10000 * 101 + 1;
};