812. Largest Triangle Area
1. Description
Given an array of points on the X-Y plane points where points[i] = [xi, yi], return the area of the largest triangle that can be formed by any three different points. Answers within 10-5 of the actual answer will be accepted.
2. Example
Example 1: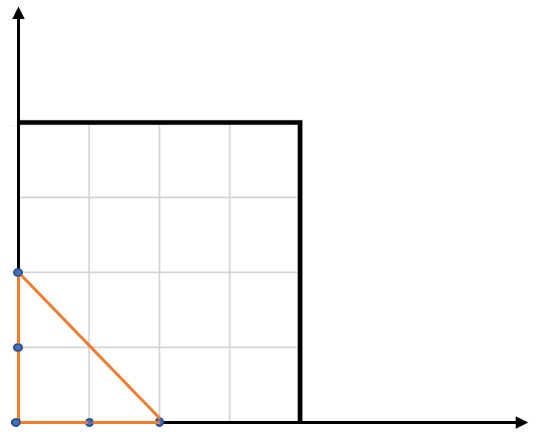
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2.00000
Explanation: The five points are shown in the above figure. The red triangle is the largest.
Example 2:
Input: points = [[1,0],[0,0],[0,1]]
Output: 0.50000
3. Constraints
- 3 <= points.length <= 50
- -50 <= , <= 50
- All the given points are unique.
4. Solutions
Brute Force
n = points.size()
Time complexity: O()
Space complexity: O(1)
class Solution {
public:
double largestTriangleArea(const vector<vector<int>>& points) {
double result = 0;
for (int i = 0; i < points.size() - 2; ++i) {
for (int j = i + 1; j < points.size() - 1; ++j) {
for (int k = j + 1; k < points.size(); ++k) {
int x1 = points[i][0], y1 = points[i][1];
int x2 = points[j][0], y2 = points[j][1];
int x3 = points[k][0], y3 = points[k][1];
result = max(result, 0.5 * abs(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2)));
}
}
}
return result;
}
};
