840. Magic Squares In Grid
1. Description
A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
Given a row x col grid of integers, how many 3 x 3 “magic square” subgrids are there? (Each subgrid is contiguous).
2. Example
Example 1: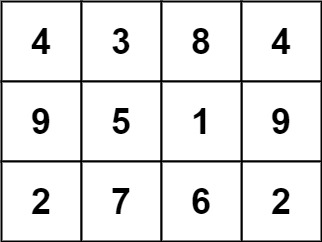
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]
Output: 1
Explanation:
The following subgrid is a 3 x 3 magic square: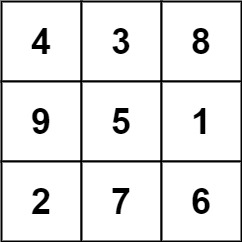
while this one is not: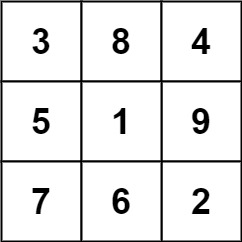
In total, there is only one magic square inside the given grid.
Example 2:
Input: grid = [[8]]
Output: 0
Example 3:
Input: grid = [[4,4],[3,3]]
Output: 0
Example 4:
Input: grid = [[4,7,8],[9,5,1],[2,3,6]]
Output: 0
3. Constraints
- row == grid.length
- col == grid[i].length
- 1 <= row, col <= 10
- 0 <= grid[i][j] <= 15
4. Solutions
My Accepted Solution
n is the number of elements in i_grid
Time complexity: O(n)
Space complexity: O(1)
class Solution {
public:
// int numMagicSquaresInside(vector<vector<int>>& grid)
int numMagicSquaresInside(const vector<vector<int>>& i_grid) {
int count = 0;
// there are two conditions to form a magic square
// the center value is 5
// the values around(from left-top one) is 18349276 or 1672943
vector<string> valueCircles = {"183492761834927", "1672943816729438"};
const int rows = i_grid.size(), columns = i_grid.front().size();
for (int row = 1; row < rows - 1; ++row) {
for (int column = 1; column < columns - 1; ++column) {
if (i_grid[row][column] == 5) {
string circle;
circle.push_back(i_grid[row - 1][column - 1] + '0');
circle.push_back(i_grid[row - 1][column] + '0');
circle.push_back(i_grid[row - 1][column + 1] + '0');
circle.push_back(i_grid[row][column + 1] + '0');
circle.push_back(i_grid[row + 1][column + 1] + '0');
circle.push_back(i_grid[row + 1][column] + '0');
circle.push_back(i_grid[row + 1][column - 1] + '0');
circle.push_back(i_grid[row][column - 1] + '0');
if (valueCircles[0].find(circle) != string::npos ||
valueCircles[1].find(circle) != string::npos) {
++count;
}
}
}
}
return count;
}
};