865. Smallest Subtree with all the Deepest Nodes

1. Description

Given the root of a binary tree, the depth of each node is the shortest distance to the root.
Return the smallest subtree such that it contains all the deepest nodes in the original tree.
A node is called the deepest if it has the largest depth possible among any node in the entire tree.
The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.

2. Example

Example 1: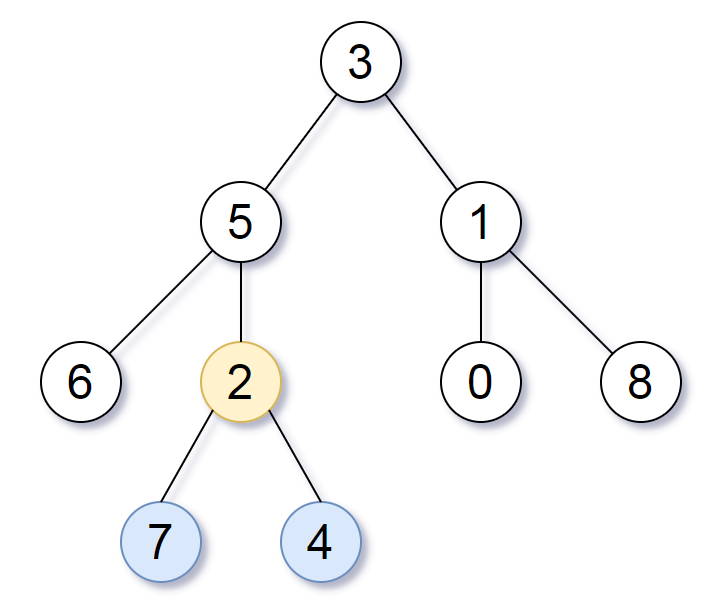

Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:
Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:
Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

3. Constraints

• The number of nodes in the tree will be in the range [1, 500].
• 0 <= Node.val <= 500
• The values of the nodes in the tree are unique.

4. Solutions

Depth-First Search

n is the number of nodes in root
Time complexity: O(n)
Space complexity: O(n)

class Solution {
public:
    TreeNode *subtreeWithAllDeepest(TreeNode *root) {
        get_max_depth_(root, 0);
        return result_ == nullptr ? root : result_;
    }

private:
    int max_depth_ = 0;
    TreeNode *result_ = nullptr;

    int get_max_depth_(TreeNode *root, int depth) {
        if (root == nullptr) {
            // null should return depth rathen than 0
            return depth;
        } else {
            int current_depth = depth + 1;
            max_depth_ = max(current_depth, max_depth_);

            int left_max_depth = get_max_depth_(root->left, current_depth);
            int right_max_depth = get_max_depth_(root->right, current_depth);

            if (left_max_depth == max_depth_ && right_max_depth == max_depth_) {
                // if only one child's max depth is the max depth, then the answer is that child
                // all required nodes should have the same depth, i.e., max depth
                result_ = root;
            }

            return max(left_max_depth, right_max_depth);
        }
    }
};