883. Projection Area of 3D Shapes

1. Description

You are given an n x n grid where we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z axes.
Each value v = grid[i][j] represents a tower of v cubes placed on top of the cell (i, j).
We view the projection of these cubes onto the xy, yz, and zx planes.
A projection is like a shadow, that maps our 3-dimensional figure to a 2-dimensional plane. We are viewing the “shadow” when looking at the cubes from the top, the front, and the side.
Return the total area of all three projections.

2. Example

Example 1: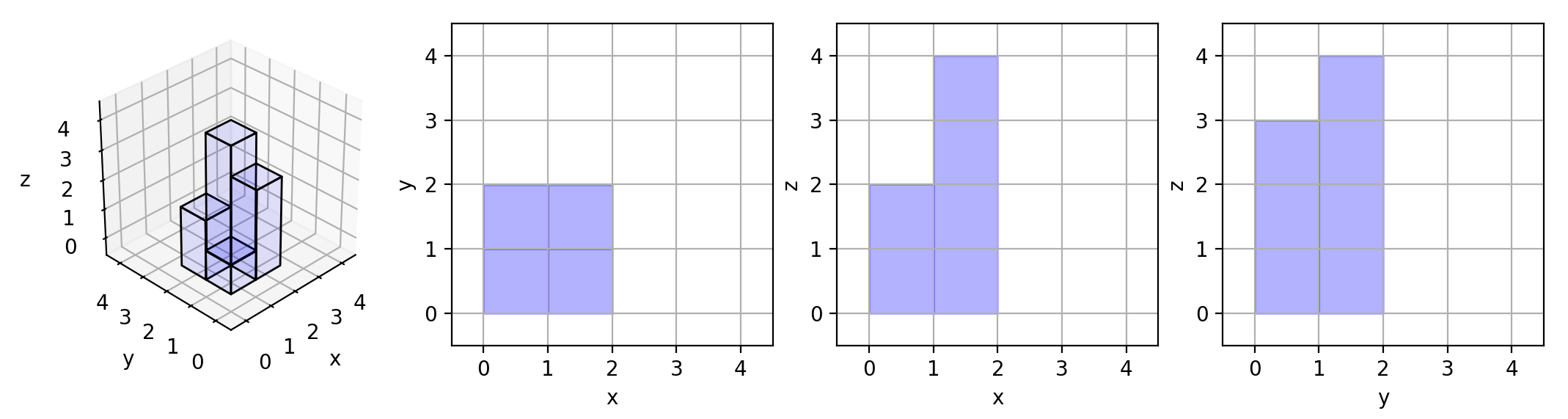

Input: grid = [[1,2],[3,4]]
Output: 17
Explanation: Here are the three projections (“shadows”) of the shape made with each axis-aligned plane.

Example 2:
Input: grid = [[2]]
Output: 5

Example 3:
Input: grid = [[1,0],[0,2]]
Output: 8

3. Constraints

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

4. Solutions

Math

n = grid.size()
Time complexity: O($n^2$)
Space complexity: O(1)

class Solution {
public:
    int projectionArea(const vector<vector<int>> &grid) {
        int xy_area = 0, xz_area = 0, yz_area = 0;
        for (int i = 0; i < grid.size(); ++i) {
            int xz_height = 0, yz_height = 0;
            for (int j = 0; j < grid.front().size(); ++j) {
                xy_area += (grid[i][j] > 0);
                xz_height = max(grid[i][j], xz_height);
                yz_height = max(grid[j][i], yz_height);
            }

            xz_area += xz_height;
            yz_area += yz_height;
        }

        return xy_area + xz_area + yz_area;
    }
};