892. Surface Area of 3D Shapes

1. Description

You are given an n x n grid where you have placed some 1 x 1 x 1 cubes. Each value v = grid[i][j] represents a tower of v cubes placed on top of cell (i, j).
After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.
Return the total surface area of the resulting shapes.
Note: The bottom face of each shape counts toward its surface area.

2. Example

Example 1:

Input: grid = [[1,2],[3,4]]
Output: 34

Example 2: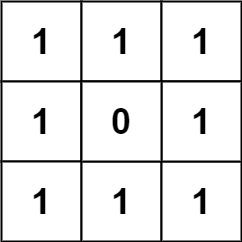

Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
Output: 32

Example 3: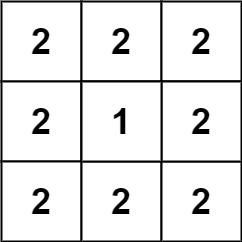

Input: grid = [[2,2,2],[2,1,2],[2,2,2]]
Output: 46

3. Constraints

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

4. Solutions

Math

n = grid.size()
Time complexity: O($n^2$)
Space complexity: O(1)

class Solution {
public:
    int surfaceArea(const vector<vector<int>> &grid) {
        int result = 0;
        for (int i = 0; i < grid.size(); ++i) {
            for (int j = 0; j < grid[i].size(); ++j) {
                result += grid[i][j] * 4 + (grid[i][j] > 0 ? 2 : 0);

                if (i > 0) {
                    result -= min(grid[i][j], grid[i - 1][j]) * 2;
                }
                if (j > 0) {
                    result -= min(grid[i][j], grid[i][j - 1]) * 2;
                }
            }
        }

        return result;
    }
};