894. All Possible Full Binary Trees
1. Description
Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.
A full binary tree is a binary tree where each node has exactly 0 or 2 children.
2. Example
Example 1: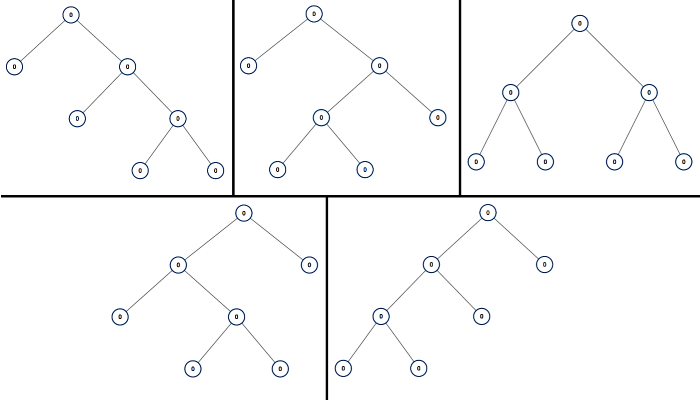
Input: n = 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Example 2:
Input: n = 3
Output: [[0,0,0]]
3. Constraints
- 1 <= n <= 20
4. Solutions
Recursion
Time complexity: O($2^n$)
Space complexity: O($2^n$)
class Solution {
public:
vector<TreeNode *> allPossibleFBT(int n) {
if (n == 1) {
return {new TreeNode()};
}
vector<TreeNode *> result;
if ((n & 1) == 1) {
for (int i = 1; i <= n; ++i) {
auto left_childs = possible_trees_.find(i - 1) != possible_trees_.end()
? possible_trees_[i - 1]
: allPossibleFBT(i - 1);
possible_trees_[i - 1] = left_childs;
auto right_childs = possible_trees_.find(n - i) != possible_trees_.end()
? possible_trees_[n - i]
: allPossibleFBT(n - i);
possible_trees_[n - i] = right_childs;
if (!left_childs.empty() && !right_childs.empty()) {
for (auto left : left_childs) {
for (auto right : right_childs) {
auto root = new TreeNode();
root->left = left;
root->right = right;
result.push_back(root);
}
}
}
}
}
return result;
}
private:
unordered_map<int, vector<TreeNode *>> possible_trees_;
};