919. Complete Binary Tree Inserter
1. Description
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the CBTInserter class:
- CBTInserter(TreeNode root) Initializes the data structure with the root of the complete binary tree.
- int insert(int v) Inserts a TreeNode into the tree with value Node.val == val so that the tree remains complete, and returns the value of the parent of the inserted TreeNode.
- TreeNode get_root() Returns the root node of the tree.
2. Example
Example 1: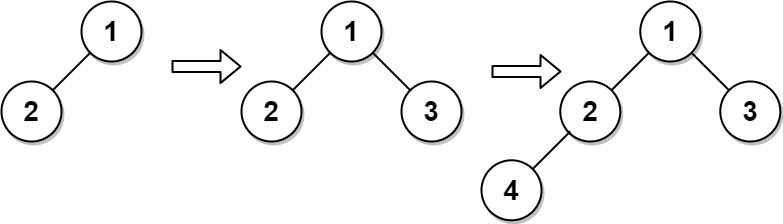
Input
[“CBTInserter”, “insert”, “insert”, “get_root”]
[[[1, 2]], [3], [4], []]
Output
[null, 1, 2, [1, 2, 3, 4]]
Explanation
CBTInserter cBTInserter = new CBTInserter([1, 2]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get_root(); // return [1, 2, 3, 4]
3. Constraints
- The number of nodes in the tree will be in the range [1, 1000].
- 0 <= Node.val <= 5000
- root is a complete binary tree.
- 0 <= val <= 5000
- At most 104 calls will be made to insert and get_root.
4. Solutions
Binary
class CBTInserter {
public:
CBTInserter(TreeNode *root) {
root_ = root;
node_count_ = count_nodes_(root);
}
int insert(int val) {
if (++node_count_ > ((1 << depth_) - 1)) {
++depth_;
}
int digit = depth_ - 1 - 1;
auto iter = root_;
for (; digit > 0; --digit) {
iter = (node_count_ & (1 << digit)) == 0 ? iter->left : iter->right;
}
auto node_to_insert = new TreeNode(val);
(node_count_ & 1) == 0 ? iter->left = node_to_insert : iter->right = node_to_insert;
return iter->val;
}
TreeNode *get_root() {
return root_;
}
private:
TreeNode *root_;
int depth_;
int node_count_;
int count_nodes_(TreeNode *root) {
if (root != nullptr) {
depth_ = 0;
for (auto iter = root; iter != nullptr; iter = iter->left) {
++depth_;
}
int nodes_count = 1;
int min_border = 1 << (depth_ - 1);
int max_border = (1 << depth_) - 1;
for (int left = min_border, right = max_border, mid = (min_border + max_border) / 2;
left <= right;
mid = (left + right) / 2) {
int digit = depth_ - 1 - 1;
auto iter = root;
for (; digit >= 0; --digit) {
iter = (mid & (1 << digit)) == 0 ? iter->left : iter->right;
}
iter != nullptr ? nodes_count = mid, left = mid + 1 : right = mid - 1;
}
return nodes_count;
} else {
return 0;
}
}
};