938. Range Sum of BST

1. Description

Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].

2. Example

Example 1: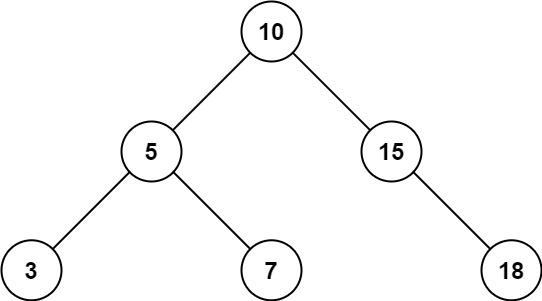

Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2: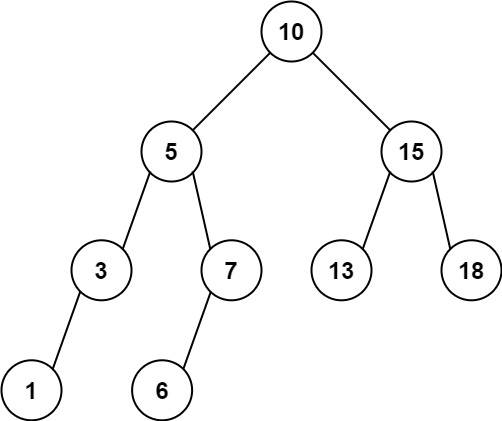

Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23
Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

3. Constraints

• The number of nodes in the tree is in the range [1, $2 * 10^4$].
• 1 <= Node.val <= $10^5$
• 1 <= low <= high <= $10^5$
• All Node.val are unique.

4. Solutions

Depth-First Search

n is the number of nodes in root
Time complexity: O(n)
Space complexity: O(n)

class Solution {
public:
    int rangeSumBST(TreeNode *root, int low, int high) {
        if(root == nullptr) {
            return 0;
        }

        if(root->val < low) {
            return rangeSumBST(root->right, low, high);
        } else if(root->val > high) {
            return rangeSumBST(root->left, low, high);
        }

        return root->val + rangeSumBST(root->right, low, high) + rangeSumBST(root->left, low, high);
    }
};