951. Flip Equivalent Binary Trees

1. Description

For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.

2. Example

Example 1: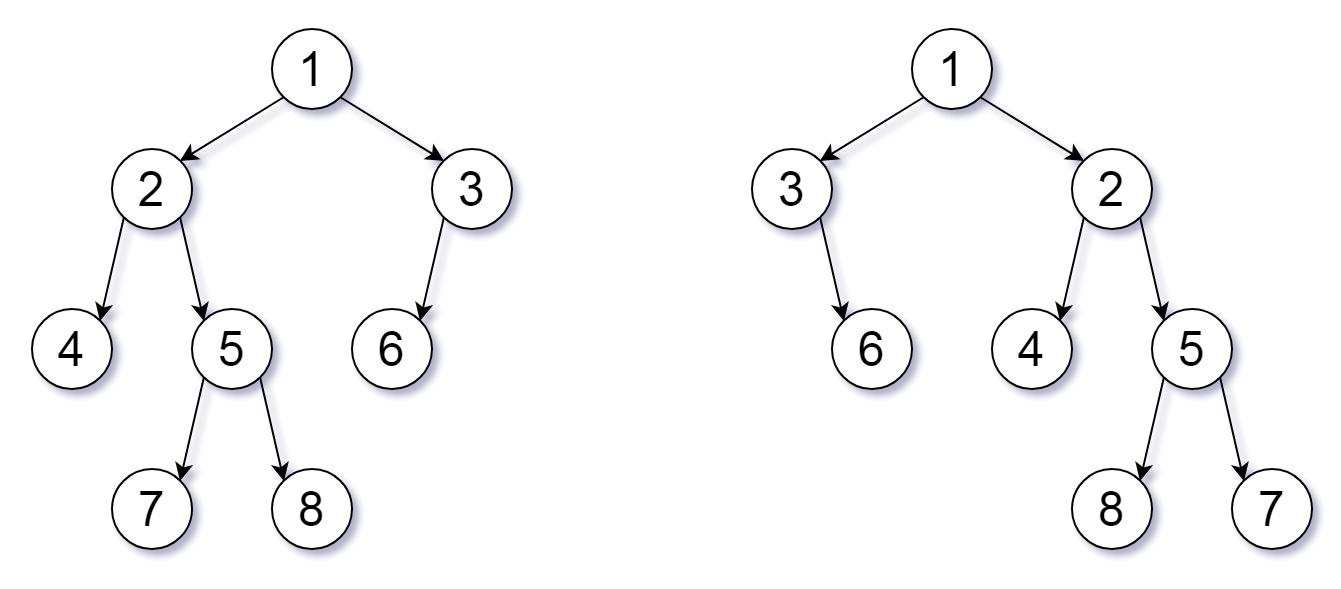

Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.

Example 2:
Input: root1 = [], root2 = []
Output: true

Example 3:
Input: root1 = [], root2 = [1]
Output: false

3. Constraints

• The number of nodes in each tree is in the range [0, 100].
• Each tree will have unique node values in the range [0, 99].

4. Solutions

Depth-First Search

n is the number of nodes in root, h is the height of root
Time complexity: O(min(n1, n2))
Space complexity: O(min(h1, h2))

class Solution {
public:
    bool flipEquiv(TreeNode *root1, TreeNode *root2) {
        if (root1 == nullptr && root2 == nullptr) {
            return true;
        } else if (root1 == nullptr || root2 == nullptr) {
            return false;
        } else {
            if (root1->val != root2->val) {
                return false;
            }

            if ((root1->left == nullptr && root2->right == nullptr) ||
                (root1->left != nullptr && root2->right != nullptr &&
                 root1->left->val == root2->right->val)) {
                swap(root2->left, root2->right);
            }

            return flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right);
        }
    }
};